Czytaj książkę: «Квантовая химия в примерах»

© Игорь А. Мерзляков, 2025

ISBN 978-5-4498-2768-5

Создано в интеллектуальной издательской системе Ridero

1. Введение

Термин «кристаллография» впервые был предложен швейцарским учёным М. Капеллером в 1723 году. На сегодняшний день значительная доля специалистов по анализу и по классификации химических соединений, несмотря ни на какие обстоятельства, продолжает изучать особенности строения встречающихся в природе минералов, пытаясь решить в общем виде задачу «компактной упаковки шаров». Разумеется, исходя из условий затронутой здесь задачи, шары нужно во что бы то ни стало поместить в прямоугольный ящик. Одновременно с этим свободное пространство, существующее между рассматриваемыми геометрическими фигурами, должно быть минимальным. Несомненно, цель такого рода действий состоит в выделении основных типов кристаллических решёток. Однако для сложной химической структуры часто остаются открытыми вопросы о диаметрах шаров и о габаритах той упаковки, куда помещаются указанные предметы, поскольку именно радиус интересующей нас сферы определяет вид атома, а линейные размеры ящика дают информацию о будущих свойствах построенной в каждом конкретном случае решётки Браве.

В этой работе мы разберём целый ряд методов, ориентированных как на предсказание кристаллов, молекул, аморфных тел и прочих структур, так и на прогнозирование химических реакций. В итоге, сконструировав специальное устройство и выяснив, пусть даже приблизительно, термодинамические параметры окружающей среды, в которой в конечном счёте произойдёт химический синтез моделируемого вещества на практике, нам останется всего-навсего подтвердить или опровергнуть выдвинутое ранее предположение касательно возможности образования спроектированного материала в реальности. Если временную эволюцию изолированной от внешнего воздействия квантовой системы не удастся описать математически, то составленную из атомов кристаллическую решётку или созданную похожим путём молекулу нельзя будет получить в лаборатории.

Приятного чтения!

2. Моделирование кристаллов и молекул

Во 2-й главе настоящей монографии мы рассмотрим состоящие из 2-х атомов, имеющих квантовые уровни под номером h=2, химические соединения. В периодической таблице Менделеева наименования исследуемых химических элементов расположены во втором периоде. Последний включает в себя одиночные ионы, начиная от лития Li⁺ и заканчивая неоном Ne⁰. Бесспорно, на картинках 2.1, 2.2, 2.3, а также 2.4 можно увидеть фрагменты молекулярных или кристаллических структур, сконструированные из взаимодействующих друг с другом фермионов и бозонов.

Рисунок 2.1 Наглядный пример пересечения 2-х кубов в окрестностях их вершин.

Обозначим крестиками те потенциальные ямы, в которые попадут электроны. Пустые потенциальные ямы, участвующие в образовании химических связей между соответствующими атомами, выделим треугольниками. К слову сказать, в центре каждого из изучаемых в настоящем параграфе химических элементов можно обнаружить положительно заряженное ядро. Области синусоидальной функции A``=П_Θ=1³sin (πm_Θx_Θ/R_Θ), где крестики и треугольники объединятся между собой, отметим звёздочками.

Итак, на чертеже 2.1 продемонстрированы 2 пары одиночных ионов, расположенных отдельно друг от друга на размещённом слева рисунке и скреплённых в общую химическую структуру на запечатлённом справа изображении. Далее рассмотрим материальные частицы, визуализированные на эскизе 2.2. Вне всякого сомнения, треугольники, сосредоточенные внутри первого бозона, лежат на одной прямой, вследствие чего в них легко попадают крестики (потенциальные ямы с электронами (в дальнейшем лептонами или фермиономи)) другого химического элемента. Таким образом, на иллюстрации 2.2 возможно увидеть более прочное соединение по сравнению с тем, что было показано на картинке 2.1.

Рисунок 2.2 Наглядный пример пересечения 2-х правильных шестигранников вдоль целого семейства проведённых через точки A``=0 вертикальных отрезков, когда z=R_z/ (2m_z).

Кстати говоря, наиболее стабильная химическая связь, которая только способна возникнуть между атомами заданной кристаллической структуры или нейтральной молекулы, может сформироваться исключительно при совмещении подходящей пары ионов вдоль 2-х построенных перпендикулярно горизонтальному сечению синусоидальной функции A`` и вместе с тем удовлетворяющих соотношению A``=0 параллельных плоскостей, если z=R_z/ (2m_z). Конечно, на чертеже 2.3 продемонстрировано соединение такого рода. Как несложно заметить, на изображении 2.3 в центрах граней взаимодействующих между собой атомов локализованы треугольники. Вообще, данное обстоятельство указывает лишь на то, что синтезированный в природе материал будет проявлять себя как дырочный полупроводник.

Рисунок 2.3 Возможный вариант объединения 2-х правильных прямоугольных параллелепипедов вдоль их граней.

Теперь обратимся к эскизу 2.4. По идее, силы Ван-дер-Ваальса, которые чаще всего возникают при поляризации молекул, а также при образовании диполей, надо учитывать только в том случае, когда абсолютно все имеющиеся в составе исследуемой здесь квантовой системы треугольники окажутся заполненными электронами. Разумеется, ярким примером рассматриваемого сейчас вещества может послужить графен. На практике двумерные кристаллы графена начнут притягиваться друг к другу, образуя трёхмерное химическое соединение графита. Причём Ван-дер-Ваальсово взаимодействие надлежащих частиц будет вносить хоть сколько-нибудь заметный вклад в формирование изучаемой на этом этапе химической структуры тогда и только тогда, когда общая площадь поверхности соприкосновения монослоёв углерода C устремится непосредственно в сторону возрастания своего значения вплоть до достижения некоторого максимума. Безоговорочно, катионы и анионы, закреплённые в узлах всякого устойчивого химического соединения, останутся неподвижными в пространстве потенциальных ям до тех пор, пока не изменятся полупериоды R_x/m_x, R_y/m_y, R_z/m_z, а также R_r/m_r, R_θ/m_θ, R_φ/m_φ интересующих нас синусоидальных функций A`` или B``=sin (πm_rr/R_r) sin (πm_θθ/R_θ) sin (πm_φφ/R_φ).

Рисунок 2.4 Ван-дер-Ваальсова связь.

Если хотя бы один из визуализированных на чертежах 2.1, 2.2 и 2.3 треугольников окажется незанятым тем или иным отрицательно заряженным лептоном, то синтез исследуемой в данный момент химической структуры не получится реализовать в природе. Исключениями, судя по всему, являются те потенциальные ямы, которые, с одной стороны, могут вызвать дырочную проводимость в кристалле, а с другой – будут соответствовать полностью и иногда ровно наполовину свободным подуровням, относящимся собственно к h и более высоким h+1, h+2,…,h+g (g∈N) уровням изучаемого в каждом конкретном случае химического элемента. Примечательно, что для единичного иона натрия Na⁺, заключённого внутри металла Na₂He, 3d¹⁰ орбиталь по факту останется пустой (см. раздел 3 «„Запрещённая химия“ А. Р. Оганова»). В целом, разобранный выше подход не составит большого труда применить на практике как для моделирования молекул, так и для предсказания кристаллических решёток.

3. «Запрещённая химия» А. Р. Оганова

Как известно, опираясь на эволюционный алгоритм, предложенный А. Р. Огановым, можно с лёгкостью разработать проект практически любой существующей под высоким давлением P_b> 10⁴ МПа кристаллической структуры. «Запрещённые» химические соединения, сконструированные с помощью специально созданной в лаборатории Оганова компьютерной программы «USPEX», как правило, бывают либо двумерными (слоистыми), либо трёхмерными. В 9-м разделе этого пособия мы опишем основные свойства исследуемых в главах 3, 4, 5 и 6 решёток Браве. Совершенно ясно, что время t, отведённое на прогнозирование каждого из анизотропных кристаллов, в подавляющем большинстве случаев будет зависеть не только от суммы участвующих в расчёте частиц, но и от общего количества удовлетворяющих требованиям компактности, симметрии и периодичности квантовых систем.

Принципы, положенные в основу моделирования кристаллических решёток, аморфных тел и так далее:

а) Без сомнения, во всяком устойчивом химическом соединении не должно присутствовать пустых потенциальных ям, в которые рано или поздно попадут отрицательно заряженные электроны. Тем не менее исключениями являются абсолютно все незанятые лептонами потенциальные ямы, соответствующие полностью, а также ровно наполовину свободным подуровням, имеющимся в составе орбитальной диаграммы каждого из зафиксированных в узлах надлежащей элементарной ячейки атомов. Безоговорочно, прибегая к формулам (8.1) или (8.2) (см. раздел 8 [1]), возможно определить минимальное число локализованных в том или ином одиночном ионе треугольников. Вдобавок ко всему, необходимо дополнительно взять в расчёт сумму тех потенциальных ям, которые будут отвечать за дырочную проводимость, если последняя появится в веществе.

б) Неудивительно, что внутри абсолютно любого однородного материала всегда наблюдается симметрия. Беспрекословно, при выполнении настоящего условия во всякой изолированной от внешнего воздействия квантовой системе обязательно установится электростатическое равновесие между положительными ядрами и отрицательными лептонами.

в) Конечно, конструктивные элементы молекул или кристаллических решёток должны располагаться в пространстве потенциальных ям наиболее компактным образом друг относительно друга. Если исследуемая здесь атомная структура окажется менее компактной, чем прочие химические соединения, обладающие похожим набором простых и/или сложных ионов, то предсказанное ранее вещество нельзя будет синтезировать в лаборатории.

г) Итак, кристаллы характеризуются строгой пространственной периодичностью в расположении составляющих их материальных частиц. Под периодичностью понимают повторяемость элементов решётки в том или ином направлении. Очевидно, что указанное требование не распространяется на квазикристаллы.

В случае, когда построенная из атомов химическая структура будет удовлетворять разобранным в пунктах а), б), в) и г) правилам, тогда полная энергия надлежащей квантовой системы E_p примет минимальное значение E_p=min. Таким образом, в реальных природных условиях катион водорода H⁺, например, устремится к центру грани другого присоединяемого непосредственно к изучаемому гидрогену H⁺ химического элемента.

3.1 Динатриевый гелид

В этом параграфе мы рассмотрим металл Na₂He, существующий под высоким давлением P_b≈113 ГПа. В дальнейшем на эскизах 3.1—6.2 жирным шрифтом будут обозначаться наименования закреплённых в узлах исследуемых химических соединений видимых ядер, а обычным – невидимых. Теперь отыщем сумму треугольников, сосредоточенных внутри каждого из нейтральных ионов гелия He⁰, тогда:

Tr (He) =0

Для натрия Na целую положительную величину Tr (Na) можно определить из математического выражения:

Tr (Na) =48—11+10—30=17

здесь 48 – расчётное количество заполненных и незаполненных потенциальных ям, расположенных на наружной оболочке проектируемого в настоящий момент гексаэдра (атома) уровня h=3 (см. таблицу 8.1 столбец 3 [1]);

11 – порядковый номер натрия Na, взятый из периодической таблицы Менделеева;

10=30/3 – ядерный заряд бозона неона Ne;

30 – трёхкратное количество электронов, сгруппированных на скрытых оболочках интересующего нас куба уровней h=1 и h=2.

Так вот, основные компоненты элементарной ячейки динатриевого гелида Na₂He продемонстрированы на изображениях 3.1 и 3.2.

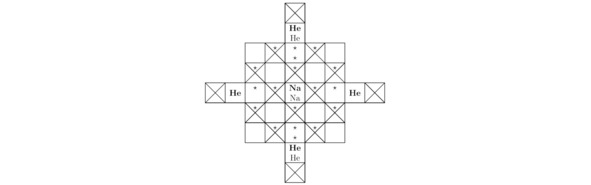
Рисунок 3.1 Вид «спереди» для кристалла Na₂He.

Рисунок 3.2 Вид «сверху» для моделируемой на этом этапе химической структуры.

Далее вычислим минимальное количество крестиков Kr (Na) для натрия Na, следовательно:

Kr (Na) =48—17=3

Для гелия He натуральный коэффициент Kr (He) будет равен:

Kr (He) =2

В процессе формирования кристаллической решётки динатриевого гелида Na₂He относящийся собственно к самой орбитальной диаграмме каждого из атомов натрия Na 3d¹⁰ подуровень по факту останется пустым. Таким образом, искомое значение дискретной переменной Tr (Na) составит:

Tr (Na) =17—10=7

где 17 – сумма заключённых внутри катиона натрия Na⁺ незанятых потенциальных ям, а 10 – полное число фигурирующих на 3d¹⁰ орбитали и вместе с тем ограниченных со всех сторон проведёнными через точки A``=0 прямыми или кривыми линиями областей конкретно заданной синусоидальной функции A`` <0.

Для того чтобы найти общее количество треугольников Tr (Na), содержащихся в единичном ионе натрия Na⁺, необходимо дополнительно взять в расчёт 2 отрицательно заряженные частицы, вытесненные на 4-й квантовый уровень h=4, тогда Tr (Na) =7+2=9. Если 3p⁶ подуровень, принадлежащий внешней оболочке фермиона натрия Na (правильного шестигранника), окажется полностью свободным, то в этом случае математическая величина Tr (Na) примет следующее значение: Tr (Na) =9-6-2=1. Почти всегда в ходе неравномерного преобразования формы пространства потенциальных ям внутренняя энергия u, определяемая для исследуемого твёрдого тела, будет изменяться во времени t. К тому же каждый из атомов изучаемой здесь химической структуры во что бы то ни стало начнёт перемещаться относительно того или иного неподвижного объекта в сторону минимизации физического параметра E_p-> min. Если полупериоды R_r/m_r, R_θ/m_θ и R_φ/m_φ соответствующей синусоидальной функции B`` стабилизируются, то изолированная от внешнего воздействия квантовая система перейдёт из нестационарного состояния в стационарное или в квазистационарное.